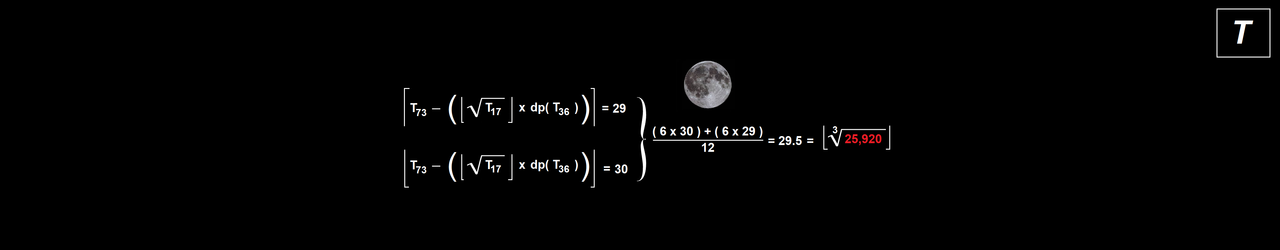A History of Figurate Numbers
Sept 27, 2020 19:31:18 GMT
Post by Admin on Sept 27, 2020 19:31:18 GMT
.
NOTES are in folder titled " computus and figurates " in " my forum " folder
-------------------



Regrettably, Dicuil did not identify his sources for his Computus. In section 2 of the chapter under discussion he mentions the ‘philosophers’ in relation to triangular numbers, but he copied this from Isidore of Seville (Esposito 1920–21). According to Esposito, Dicuil would have had access to many encyclopaedic, astronomical and computistical works in Latin at the Frankish court, including those of Pliny the Elder (d. 79 AD), Victorius of Aquitaine (fifth century), Dionysius Exiguus (sixth century), Isidore of Seville (c. 600), Bede (c. 672–735), Alcuin (c. 735–804) and many authors now lost to us
None of the authors named above mentions triangular numbers, except Isidore (Barney et al. 2006) who lists them among the planar
numbers in his Etymologies (Book III, chapter 7, section 4), but does not go into details. Several texts from the computus congress of 809 made use of an anonymous seventh century Irish tract, De ratione conputandi, but Dicuil did not use that tract (Walsh and Ó Cróinin 1988, 103). Neither did he use Bede’s De ratione temporum (Bergmann 1993). He did refer to works often attributed to Alcuin – De cursu et saltu lunae and De bissexto – but these works were probably not by Alcuin (Lohrmann 1993; Springsfeld 2002, 64–79). Dicuil’s use of these works was only to criticize them (Bergmann 1993)
Dicuil preferred his native Irish dating system to the English method, and claimed in Book 1, chapter 5, section 2, that his system was based on the rules of the Greeks and Romans (Cordoliani 1960, 334 and footnote 38)
Dicuil must have been familiar with the book by Boethius (c. 500) De institutione arithmetica (On arithmetic) (Masi 1983; Oosthout and Schilling 1999), which was widely available in Western Europe. Boethius wrote in Latin, but based his book on earlier Greek authors such as Theon of Smyrna and Nicomachus. The Introduction to arithmetic by Nicomachus was translated into Latin by Apuleius in the second century (Midonick 1968, 15–16), and Boethius probably had access to this. Boethius discusses figurate numbers in Book II. He states that triangular numbers are the basis of all other figurate numbers (chapters 6 and 18). Unity is the mother of all numbers, and not a real triangular number: 3 is the first triangular number, and has 2 as a side; 6 is the second and has 3 as a side; the sides grow by unity (chapters 7 and 8). The sequence of triangular numbers grows by addition of the natural numbers (chapter 9). Later chapters deal with square numbers and other figurate numbers. He describes rectangular or heteromecic numbers (chapter 26), and says that the sum of two consecutive triangular numbers is a square number (chapters 18 and 28); but he does not give the multiplication formula, or state that a rectangular number is twice a triangular number. However, these formulae can readily be deduced from this book, so Dicuil probably benefitted from reading Boethius
Cassiodorus (c. 485–585) wrote Institutions of divine and secular learning, and on the soul (Halporn and Vessey 2004) in which he briefly mentioned triangular
numbers (Book 2, Part 4, Section 6), but not the multiplication formula. This book was not widely used or cited by Carolingian authors (Halporn and Vessey 2004, 82). Butzer (1993) concludes that the major mathematical contributions of the Carolingian period were: the pseudo-Boethian Geometry I, perhaps produced in Corbie (c.780– 800); the Libellus annalis of 793, a precursor of the Computus of 809, probably written by Alcuin; the Seven Book Computus, assembled at Aachen 809/10; and the Propositiones ad acuendos iuvenes, the oldest collection of mathematical exercises written in Latin, probably by Alcuin. We shall now turn our attention to the last of these, because it contains an example of relevance to the multiplication formula
A different tradition from the mathematical textbook lay in collections of practical problems and riddles. The multiplication formula can be used for the sum of the natural numbers in other contexts besides triangular numbers. One example occurs in Propositiones ad acuendos juvenes (Problems to sharpen the young), an early collection of recreational mathematical problems (Folkerts 1978; Hadley and Singmaster 1992; Folkerts and Gerike 1993). Problem 42 is of particular interest. It is entitled Propositio de scala habente gradus centum ( Problem concerning a staircase with a hundred steps )
A version of the multiplication formula was indeed known to the Egyptians, as early as 300 BC (Gillings 1978; Høyrup 2008). A papyrus in the British Museum contains mathematical problems, including the sum of the arithmetical progression formed by the natural numbers
Here is the translation of Dicuil's 9th century text:

Speculating whether or not Dicuil could have read Greek texts containing the use or mention of figurates can allow one to make a logical inference that he did indeed, but real question is, if he didn't list his sources, how can we reasonably infer what they were, and if not, where at least they may have come from, and who passed the knowledge down
We can do this by starting with the school the Dicuil taught at, the Carolingian school of Louis the Pious
Louis the Pious (778 – 20 June 840), also called the Fair, and the Debonaire, was the King of the Franks and co-emperor with his father, Charlemagne, from 813
He had a twin brother named Lothair, who died young. Louis and Lothair were given names from the old Merovingian dynasty, possibly to suggest a connection

Under the Merovingian Kings of the Frankish kingdoms there was established at the court a 'palatial' school -- scola palatina, the chroniclers of the eighth century styled it—for the training of the young Frankish nobles in the art of war and in the ceremonies of the court
With the accession of the future emperor Charlemagne (768) a scheme of educational reform was inaugurated, first in the palace school itself, and later in the various schools established or reformed by imperial decrees throughout the vast empire over which Charlemagne reigned. The reform of the palace school, i.e. the change from a school of military tactics and court manners to a place of learning, was begun in 780, as soon as the victories over the Lombards, Saxons and Saracens (in Iberia) afforded
Associated with the extension and promotion of the Carolingian revival of education are the names of various Irish teachers, competitors of Alcuin, who certainly share in the credit of having been the first masters of the schools. According to the St. Gall chronicler who wrote the Life of Charlemagne dedicated to Charles the Fat (d. 888), two Irish monks arrived in France before Alcuin had received Charlemagne's invitation. Having set out their stall in the marketplace to somewhat boastfully teach wisdom, they were received by the emperor with honour, and one of them placed at the head of the palace school. The story, however, is not accepted as entirely reliable.
We know for certain that after Alcuin left the court of Charlemagne, one of these monks Clement the Irishman (Clemens Scotus) succeeded him as master of the palace school, and that he had pupils sent to him even from the monastery of Fulda. The grammarian Cruindmelus, the poet Dungal of Bobbio and Bishop Donatus of Fiesole were among the many Irish teachers on the Continent who enjoyed the favour of Charlemagne. The anonymous Hibernicus exul also wrote at his court. Indeed, the emperor, according to Einhard, "loved the strangers" and "had the Irish in special esteem".
His successors likewise invited the Irish teachers to their court. Louis the Pious was the patron of the Irish geographer Dicuil, Lothair II stood in a similar relation to the Irish poet and scribe Sedulius Scottus, founder of the school at Liège, and Charles the Bald equalled his grandfather in his affectionate esteem for the Irish teachers. Under him Elias taught at Laon, Dunchad at Reims, Israel at Auxerre, and the greatest of all the Irish scholars, Johannes Scotus Eriugena, was head of the palace school.
Naturally the Irish teachers flocked to the places already known to them by the missionary activity of their fellow-countrymen of former generations We find them at Reichenau, St. Gall and Bobbio, "a whole herd of philosophers" as a ninth-century writer expresses it. Every monastery or cathedral school at which they appeared soon showed the effect of their influence. To the curriculum already in vogue in the Carolingian Schools the Irish teachers added the study of Greek, and wherever they taught philosophy or theology (dialectic and the interpretation of the Scriptures) they drew largely from the writings of the neo-Platonists and from the works of the Greek Fathers
Neo-Platonists seem to originate with Ammonius Saccas and his student Plotinus (c. 204/5 – 271 AD) and which stretches to the 5th century AD
Those who wrote in Greek are called the Greek (Church) Fathers. In addition to the Apostolic Fathers, famous Greek Fathers include: Justin Martyr, Irenaeus of Lyons, Clement of Alexandria, Athanasius of Alexandria, John Chrysostom, Cyril of Alexandria, the Cappadocian Fathers (Basil of Caesarea, Gregory Nazianzus, Gregory of Nyssa), Peter of Sebaste, Maximus the Confessor, and John of Damascus.
Justin Martyr c. 100 – c. 165
John of Damascus c. 675 - c 749
Hibernicus exul (fl. 8th century) was an anonymous Irish Latin poet, grammarian, and dialectician. His works include a comic mock epic, a panegyric to Charlemagne, epigrams of advice to young scholars and a poetic overview of the seven liberal arts
Dungal of Bobbio (fl. 811–828) was an Irish monk, teacher, astronomer, and poet. He was to live at Saint-Denis, Pavia, and Bobbio
He may be the same person as Hibernicus exul. A letter of Alcuin appears to identify him as a bishop
Saint Donatus (Donat, Donnchad) of Fiesole was an Irish teacher and poet, and Bishop of Fiesole, about 829–876
John Scotus Eriugena or Johannes Scotus Erigena (c. 800 – c. 877) was an Irish theologian, neoplatonist philosopher, and poet. He succeeded Alcuin of York (735–804) as head of the Palace School at Aachen
Bertrand Russell called him " the most astonishing person of the ninth century "
A tradition, largely considered spurious, says he was stabbed to death by his students at Malmesbury with their pens
He also translated and made commentaries upon the work of Pseudo-Dionysius, and was one of the few Western European philosophers of his day who knew Greek, having studied in Byzantine Athens
Johannes Scotus Eriugena was an Irishman, educated in Ireland. He moved to France (about 845) and took over the Palace School at the invitation of Carolingian King Charles the Bald. He succeeded Alcuin of York (735–804) as head of the Palace School. The reputation of this school, part of the Carolingian Renaissance, seems to have increased greatly under Eriugena's leadership, and the philosopher himself was treated with indulgence by the king. Whereas Alcuin was a schoolmaster rather than a philosopher,...
Eriugena was a noted Greek scholar, a skill which, though rare at that time in Western Europe, was used in the learning tradition of Early and Medieval Ireland, as evidenced by the use of Greek script in medieval Irish manuscripts
He remained in France for at least thirty years, and it was almost certainly during this period that he wrote his various works
However, what we can say is that Dicuil most likely would have learned Greek from Eriugena, being that he was a notable Greek scholar and also head of the school Dicuil himself taught at
Aachen developed from a Roman settlement and spa, subsequently becoming the preferred medieval Imperial residence of Emperor Charlemagne of the Frankish Empire,and, from 936 to 1531, the place where 31 Holy Roman Emperors were crowned Kings of the Germans
Aachen is a city of North Rhine-Westphalia
Lower Saxony : Neddersassen; Saterland Frisian: Läichsaksen) is a German state (Land) situated in northwestern Germany
Lower Saxony borders on (from north and clockwise) the North Sea, the states of Schleswig-Holstein, Hamburg, Mecklenburg-Vorpommern, Brandenburg, Saxony-Anhalt, Thuringia, Hesse and North Rhine-Westphalia, and the Netherlands (Drenthe, Groningen and Overijssel)
Elias taught at Laon, Dunchad at Reims, Israel at Auxerre
scribe Sedulius Scottus, founder of the school at Liège
The Merovingian dynasty (/ˌmɛrəˈvɪndʒiən/) was the ruling family of the Franks from the middle of the 5th century until 751, being succeeded by the Carolingian dynasty
Curiously, there is a stark juxtaposition between the Merovingians and the Carolingians
Unlike the Anglo-Saxon royal genealogies, the Merovingians never claimed descent from a god, nor is there evidence that they were regarded as sacred
A number of royal genealogies of the Anglo-Saxon kingdoms, collectively referred to as the Anglo-Saxon royal genealogies, have been preserved in a manuscript tradition based in the 8th to 10th centuries
The genealogies trace the succession of the early Anglo-Saxon kings, back to the semi-legendary kings of the Anglo-Saxon settlement of Britain, notably named as Hengest and Horsa in Bede's Historia ecclesiastica gentis Anglorum, and further to legendary kings and heroes of the pre-migration period, usually including an eponymous ancestor of the respective lineage and converging on Woden ( Odin ). In their fully elaborated forms as preserved in the Anglo-Saxon Chronicles and the Textus Roffensis, they continue the pedigrees back to the biblical patriarchs Noah and Adam. They also served as the basis for pedigrees that would be developed in 13th century Iceland for the Scandinavian royalty
Odin is known in Old English and Old Saxon as Wōden, in Old Dutch as Wuodan, and in Old High German as Wuotan, all ultimately stemming from the Proto-Germanic theonym *Wōđanaz, meaning 'lord of frenzy', or 'leader of the possessed'
Old Norse texts portray Odin as one-eyed and long-bearded, frequently wielding a spear named Gungnir and wearing a cloak and a broad hat. He is often accompanied by his animal companions and familiars—the wolves Geri and Freki and the ravens Huginn and Muninn, who bring him information from all over Midgard—and rides the flying, eight-legged steed Sleipnir across the sky and into the underworld
Odin appears as a prominent god throughout the recorded history of Northern Europe, from the Roman occupation of regions of Germania (from c. 2 BC ) through movement of peoples during the Migration Period (4th to 6th centuries AD ) and the Viking Age (8th to 11th centuries AD )
Ross, H. E., & Knott, B. I. (2019). Dicuil (9th century) on triangular and square numbers. British Journal for the History of Mathematics, 34(2), 79–94. doi:10.1080/26375451.2019.1598687
www.tandfonline.com/doi/abs/10.1080/26375451.2019.1598687
---------------------
An Irish Teacher at the Carolingian Court: Dicuil
Mario Esposito
www.jstor.org/stable/30092449?seq=1
---------------------
en.wikipedia.org/wiki/Alcuin
Quadrivium
-------------------------------------------------------------------------
Make two lists: Authors and publications , dated
Methods and formulas , dated
-------------------------------------------------------------------------
...
Bible moralisée
There are seven surviving fully illustrated manuscripts of the Bible moralisée group;all date from the thirteenth to the fifteenth centuries and were designed for the personal use of the French royal family
--------
Moon
--------
Sun
------------------
Distances - aphelion, LDU, etc
--------------
Times
-----------------
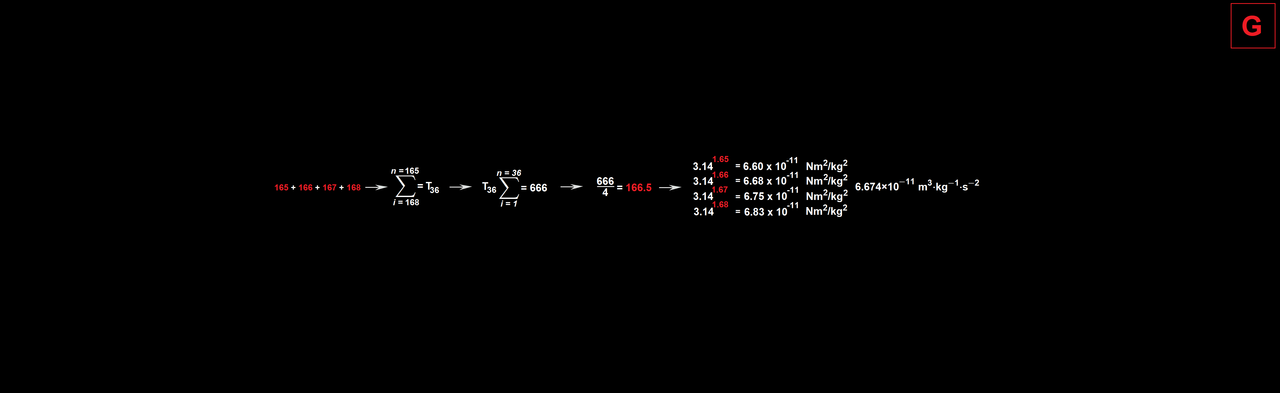
Gravity
-----------
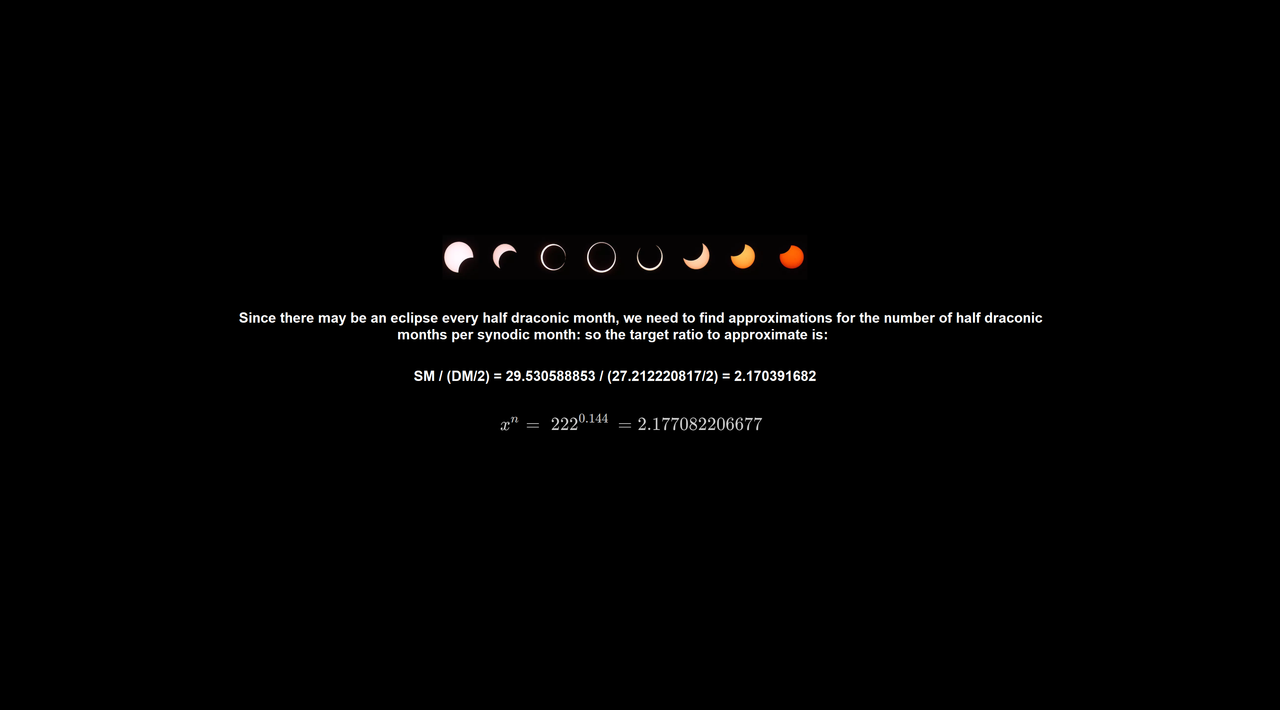
eclipses
-------------
NOTES are in folder titled " computus and figurates " in " my forum " folder
-------------------

This thread is to explore the use of figurate numbers, mainly square and triangular, in the antiquities
Figurate numbers appear in the Bible:
The number of fish caught by Jesus = 153 ( triangular figurate )
The number of the beast = 666 ( Triangular figurate )
The sum of Genesis 1:1 = 2701 ( Triangular figurate )
Starting with texts on Computus ( The calculation of the date of Easter ), specifically the 9th century Computus from the Irish monk Dicuil, we can trace both the use and study of such numbers back to early Egyptian and Sumerian society
Most folks are unaware that texts on Computus have classically included formula for generating triangular and square numbers
Figurate numbers appear in the Bible:
The number of fish caught by Jesus = 153 ( triangular figurate )
The number of the beast = 666 ( Triangular figurate )
The sum of Genesis 1:1 = 2701 ( Triangular figurate )
Starting with texts on Computus ( The calculation of the date of Easter ), specifically the 9th century Computus from the Irish monk Dicuil, we can trace both the use and study of such numbers back to early Egyptian and Sumerian society
Most folks are unaware that texts on Computus have classically included formula for generating triangular and square numbers

Dicuil was a ninth-century Irish monk who taught at the Carolingian school of Louis the Pious. He wrote a Computus or astronomical treatise in Latin in about 814–16, which contains a chapter on triangular and square numbers

In his text, he describes two methods for generating triangular numbers: the simple method of summing the natural numbers, and the more complex method of multiplication, equivalent to the formula n(n + 1)/2. He also states that a square number is equal to twice a triangular number minus the generating number, equivalent to n2 = 2[n(n + 1)/2] – n. The multiplication formula for triangular numbers was first explicitly described in about the third century AD by the Greek authors Diophantus and Iamblichus. It was also known as a solution to other mathematical problems as early as 300 BC. It reappeared in the West in the sixteenth century. Dicuil thus fills a gap in our medieval knowledge
Dicuil was most famous for writing a book on geography in 825, the Liber de mensura orbis terrae
The text is available in Latin with an English translation and commentary (Tierney 1967). The work is mainly a compilation from various sources, but contains original material on northern islands from the reports of monks who had visited the Faroe Isles and probably Iceland in the summer of 795. Dicuil spent some time in France, and certainly spent the years 814–16 at the court of Louis the Pious, Charlemagne’s successor. He was probably employed as a teacher of grammar. While there he composed a Computus or Liber de astronomia (astronomical treatise) in Latin. A computus was originally a manual for calculating the date of Easter. The date was a source of controversy between the Celtic and Roman churches: consequently, computistical studies were particularly advanced both in Britain and in Ireland (Walsh and Ó Cróinin 1988, 101–103)
Later works expanded to become general scientific encyclopaedias. One of the most influential texts was De ratione temporum (The Reckoning of Time) written by the Northumbrian scholar Bede in 725 (Wallis 1999). Charlemagne held a congress of computists at Aachen in 809 which resulted in many more works on the subject (Tierney 1967, 12). Dicuil wrote five books of computus, in mixed prose and verse. He presented the first book to King Louis as a gift in 814, on the occasion in May when annual presents were received by the monarch. It seems that he actually read aloud chapters 1–6, as he complains in a poem added later as chapter 8 (section 6) that Louis, clearly bored, paid no attention, nor even acknowledged it with a word
The chapters would not have been easy listening: the first five contain Dicuil’s innovative method of calculating the date of Easter, and chapter 6 (the subject of this paper) expounds the relation between triangular and square numbers. Dicuil presented a second unappreciated book in 815. He wrote a further two between 815 and 816, which presumably he did not present. The work has remained untranslated and little known (Esposito 1914). It does not seem to have had a wide circulation even at the time, as it is preserved in only two manuscripts, both of the ninth century: one written at the abbey of Saint Amand and now
at Valenciennes, and the other from the abbey of Saint Martin at Tours
In the Valenciennes manuscript, Dicuil’s Computus (Books 1–4 only) is the last item in a collection of treatises by various authors on miscellaneous topics, most of which are not particularly related to computus. A twelfth-century note added to the manuscript attributes the work to the more famous Alcuin. It is interesting that no contemporary names Dicuil (Manitius 1911, 648). The Tours manuscript consists of two parts: the first contains the De arithmetica and Consolatio philosophiae of Boethius, and the second contains Dicuil’s Computus with two chapters added to the fourth book, and two more chapters constituting a fifth book (also the titles of two other works by Dicuil). The last two sheets of this manuscript are now in Paris (van de Vyver 1935, 31–33; Cordoliani 1960, 325; Tannery 1967, 13–17). The Liber de astronomia had been briefly noticed by Ernest Duemmler in 1897 in his survey of the manuscripts of poetic texts
of the Carolingian Age in Valenciennes. It was first published by Esposito from the Valenciennes manuscript in 1907, with a revised edition in 1920
Little is known about Mario Esposito, except that his Italian parents moved to Dublin where he was brought up and where he became an eminent scholar of
Hiberno-Latin literature (Lapidge 1990, vii–x). Esposito himself tells us (1920–21) that he was only 19 years old when, in August 1907, he published Dicuil’s Computus, thus implying that he was born in 1886–1887. He later moved to Italy, where he died in about 1961. Esposito’s opinion of Dicuil’s Computus changed over the years. In 1907 he wrote ‘ … the whole work is full of interesting and curious information, and it is certainly surprising that it has not yet been published’. However, the work was the subject of scathing comments by Manitius (1911), who found it disorganized, with chapters following arbitrarily on each other, the author proceeding ‘in absurd fashion’ and not following even his own proposed scheme, in short ‘a work of no further interest’. He also found
Esposito’s text unsatisfactory. This negative view of the work influenced later commentators, including Esposito himself (in 1920), van de Vyver (1935, 30–31) and Cordoliani (1960, 332). The two last, however, did find some originality in the work, especially Cordoliani (332). The remarks of recent commentators tend to be more favourable: Walsh and Ó Cróinin (1988, 103) wrote ‘Dicuil’s Liber is as remarkable for its originality of content as for its structure’; and again, Ó Cróinin (2005) commented that Dicuil’s Computus ‘is remarkably original in a field where one does not expect to find such innovation in either content or form’. A very positive assessment, based on a close study of the text, has been offered by Bergmann (2011) who argues that Dicuil developed a reliable method of calculating the date of Easter using a 532-year cycle: though too late, because Bede’s inferior methods had already been accepted by the Carolingian court. Warntjes (2013) was also positive: ‘The first two decades of the ninth century saw a considerable number of original minds, the foremost among computists being the Irishman Dicuil’. None of these authors (except Bergmann) make any mention of Book I, chapter 6, concerning number sequences
The Latin list of contents gives this chapter as ‘Decrescenti numero et per semet multiplicato’. Literally this translates as ‘On increasing
numbers and numbers multiplied by themselves’, but its meaning is ‘On triangular numbers and square numbers’. This chapter is unusual in describing two methods of calculating triangular numbers: the obvious method of summation and the less familiar method of multiplication. Bergmann (2011) describes this chapter and the two formulae, and argues that it is all part of the mathematics needed for calculating the 532- year cycle
It's commonly proposed that the use of figurate numbers originated in the Pythagoreans
Unfortunately, any relevant Pythagorean writings are lost, and assumptions about Pythagorean knowledge are based on the Greek works of later authors such as Theon of Smyrna (c.115–140 AD) and Nicomachus of Gerasa (c.100 AD). These authors do not include any statement describing the formula n(n + 1)/2, and it has been argued that this formula may not have originated with the Pythagoreans but rather in the Near East (Høyrup 2008)
Theon of Smyrna wrote Mathematics useful for the understanding of Plato (Lawlor and Lawlor 1978). Theon describes triangular numbers and gives the formula by addition (Part 1, xix). He also states that the sum of two consecutive triangular numbers is a square number (Part 1, xxviii), but without giving a formula. Nicomachus wrote Arithmetike isagoge (Introduction to arithmetic) (D’Ooge 1926)
In Book II, chapter 8, he describes triangular numbers but gives only the formula by addition, with diagrams showing the number of dots in the triangles. He again states that the sum of two consecutive triangular numbers is a square number (Book II, chapter 12). Iamblichus (c. 245–325) makes a similar statement in his commentary on Nicomachus (Heath 1921, 114; Pistelli 1975, 75, lines 25–27). Another well-known Greek author of about the same period as Theon and Nicomachus was Plutarch (c. 50 – c. 120 AD). In his Moralia: Platonic questions 1003f (Loeb Classical Library 1976) he states correctly that 8 times a triangular number plus 1 is a square number. This implies some knowledge of the multiplication formula, even though Plutarch does not state that formula
There seem to be no later authors – until Dicuil in the ninth century – who describe the multiplication formula in the context of triangular numbers, and whose work is extant
Here is the periodization of Greek authors known to have included or implied knowledge of the use and generation of figurate numbers

In his text, he describes two methods for generating triangular numbers: the simple method of summing the natural numbers, and the more complex method of multiplication, equivalent to the formula n(n + 1)/2. He also states that a square number is equal to twice a triangular number minus the generating number, equivalent to n2 = 2[n(n + 1)/2] – n. The multiplication formula for triangular numbers was first explicitly described in about the third century AD by the Greek authors Diophantus and Iamblichus. It was also known as a solution to other mathematical problems as early as 300 BC. It reappeared in the West in the sixteenth century. Dicuil thus fills a gap in our medieval knowledge
Dicuil was most famous for writing a book on geography in 825, the Liber de mensura orbis terrae
The text is available in Latin with an English translation and commentary (Tierney 1967). The work is mainly a compilation from various sources, but contains original material on northern islands from the reports of monks who had visited the Faroe Isles and probably Iceland in the summer of 795. Dicuil spent some time in France, and certainly spent the years 814–16 at the court of Louis the Pious, Charlemagne’s successor. He was probably employed as a teacher of grammar. While there he composed a Computus or Liber de astronomia (astronomical treatise) in Latin. A computus was originally a manual for calculating the date of Easter. The date was a source of controversy between the Celtic and Roman churches: consequently, computistical studies were particularly advanced both in Britain and in Ireland (Walsh and Ó Cróinin 1988, 101–103)
Later works expanded to become general scientific encyclopaedias. One of the most influential texts was De ratione temporum (The Reckoning of Time) written by the Northumbrian scholar Bede in 725 (Wallis 1999). Charlemagne held a congress of computists at Aachen in 809 which resulted in many more works on the subject (Tierney 1967, 12). Dicuil wrote five books of computus, in mixed prose and verse. He presented the first book to King Louis as a gift in 814, on the occasion in May when annual presents were received by the monarch. It seems that he actually read aloud chapters 1–6, as he complains in a poem added later as chapter 8 (section 6) that Louis, clearly bored, paid no attention, nor even acknowledged it with a word
The chapters would not have been easy listening: the first five contain Dicuil’s innovative method of calculating the date of Easter, and chapter 6 (the subject of this paper) expounds the relation between triangular and square numbers. Dicuil presented a second unappreciated book in 815. He wrote a further two between 815 and 816, which presumably he did not present. The work has remained untranslated and little known (Esposito 1914). It does not seem to have had a wide circulation even at the time, as it is preserved in only two manuscripts, both of the ninth century: one written at the abbey of Saint Amand and now
at Valenciennes, and the other from the abbey of Saint Martin at Tours
In the Valenciennes manuscript, Dicuil’s Computus (Books 1–4 only) is the last item in a collection of treatises by various authors on miscellaneous topics, most of which are not particularly related to computus. A twelfth-century note added to the manuscript attributes the work to the more famous Alcuin. It is interesting that no contemporary names Dicuil (Manitius 1911, 648). The Tours manuscript consists of two parts: the first contains the De arithmetica and Consolatio philosophiae of Boethius, and the second contains Dicuil’s Computus with two chapters added to the fourth book, and two more chapters constituting a fifth book (also the titles of two other works by Dicuil). The last two sheets of this manuscript are now in Paris (van de Vyver 1935, 31–33; Cordoliani 1960, 325; Tannery 1967, 13–17). The Liber de astronomia had been briefly noticed by Ernest Duemmler in 1897 in his survey of the manuscripts of poetic texts
of the Carolingian Age in Valenciennes. It was first published by Esposito from the Valenciennes manuscript in 1907, with a revised edition in 1920
Little is known about Mario Esposito, except that his Italian parents moved to Dublin where he was brought up and where he became an eminent scholar of
Hiberno-Latin literature (Lapidge 1990, vii–x). Esposito himself tells us (1920–21) that he was only 19 years old when, in August 1907, he published Dicuil’s Computus, thus implying that he was born in 1886–1887. He later moved to Italy, where he died in about 1961. Esposito’s opinion of Dicuil’s Computus changed over the years. In 1907 he wrote ‘ … the whole work is full of interesting and curious information, and it is certainly surprising that it has not yet been published’. However, the work was the subject of scathing comments by Manitius (1911), who found it disorganized, with chapters following arbitrarily on each other, the author proceeding ‘in absurd fashion’ and not following even his own proposed scheme, in short ‘a work of no further interest’. He also found
Esposito’s text unsatisfactory. This negative view of the work influenced later commentators, including Esposito himself (in 1920), van de Vyver (1935, 30–31) and Cordoliani (1960, 332). The two last, however, did find some originality in the work, especially Cordoliani (332). The remarks of recent commentators tend to be more favourable: Walsh and Ó Cróinin (1988, 103) wrote ‘Dicuil’s Liber is as remarkable for its originality of content as for its structure’; and again, Ó Cróinin (2005) commented that Dicuil’s Computus ‘is remarkably original in a field where one does not expect to find such innovation in either content or form’. A very positive assessment, based on a close study of the text, has been offered by Bergmann (2011) who argues that Dicuil developed a reliable method of calculating the date of Easter using a 532-year cycle: though too late, because Bede’s inferior methods had already been accepted by the Carolingian court. Warntjes (2013) was also positive: ‘The first two decades of the ninth century saw a considerable number of original minds, the foremost among computists being the Irishman Dicuil’. None of these authors (except Bergmann) make any mention of Book I, chapter 6, concerning number sequences
The Latin list of contents gives this chapter as ‘Decrescenti numero et per semet multiplicato’. Literally this translates as ‘On increasing
numbers and numbers multiplied by themselves’, but its meaning is ‘On triangular numbers and square numbers’. This chapter is unusual in describing two methods of calculating triangular numbers: the obvious method of summation and the less familiar method of multiplication. Bergmann (2011) describes this chapter and the two formulae, and argues that it is all part of the mathematics needed for calculating the 532- year cycle
It's commonly proposed that the use of figurate numbers originated in the Pythagoreans
Unfortunately, any relevant Pythagorean writings are lost, and assumptions about Pythagorean knowledge are based on the Greek works of later authors such as Theon of Smyrna (c.115–140 AD) and Nicomachus of Gerasa (c.100 AD). These authors do not include any statement describing the formula n(n + 1)/2, and it has been argued that this formula may not have originated with the Pythagoreans but rather in the Near East (Høyrup 2008)
Theon of Smyrna wrote Mathematics useful for the understanding of Plato (Lawlor and Lawlor 1978). Theon describes triangular numbers and gives the formula by addition (Part 1, xix). He also states that the sum of two consecutive triangular numbers is a square number (Part 1, xxviii), but without giving a formula. Nicomachus wrote Arithmetike isagoge (Introduction to arithmetic) (D’Ooge 1926)
In Book II, chapter 8, he describes triangular numbers but gives only the formula by addition, with diagrams showing the number of dots in the triangles. He again states that the sum of two consecutive triangular numbers is a square number (Book II, chapter 12). Iamblichus (c. 245–325) makes a similar statement in his commentary on Nicomachus (Heath 1921, 114; Pistelli 1975, 75, lines 25–27). Another well-known Greek author of about the same period as Theon and Nicomachus was Plutarch (c. 50 – c. 120 AD). In his Moralia: Platonic questions 1003f (Loeb Classical Library 1976) he states correctly that 8 times a triangular number plus 1 is a square number. This implies some knowledge of the multiplication formula, even though Plutarch does not state that formula
There seem to be no later authors – until Dicuil in the ninth century – who describe the multiplication formula in the context of triangular numbers, and whose work is extant
Here is the periodization of Greek authors known to have included or implied knowledge of the use and generation of figurate numbers

Regrettably, Dicuil did not identify his sources for his Computus. In section 2 of the chapter under discussion he mentions the ‘philosophers’ in relation to triangular numbers, but he copied this from Isidore of Seville (Esposito 1920–21). According to Esposito, Dicuil would have had access to many encyclopaedic, astronomical and computistical works in Latin at the Frankish court, including those of Pliny the Elder (d. 79 AD), Victorius of Aquitaine (fifth century), Dionysius Exiguus (sixth century), Isidore of Seville (c. 600), Bede (c. 672–735), Alcuin (c. 735–804) and many authors now lost to us
None of the authors named above mentions triangular numbers, except Isidore (Barney et al. 2006) who lists them among the planar
numbers in his Etymologies (Book III, chapter 7, section 4), but does not go into details. Several texts from the computus congress of 809 made use of an anonymous seventh century Irish tract, De ratione conputandi, but Dicuil did not use that tract (Walsh and Ó Cróinin 1988, 103). Neither did he use Bede’s De ratione temporum (Bergmann 1993). He did refer to works often attributed to Alcuin – De cursu et saltu lunae and De bissexto – but these works were probably not by Alcuin (Lohrmann 1993; Springsfeld 2002, 64–79). Dicuil’s use of these works was only to criticize them (Bergmann 1993)
Dicuil preferred his native Irish dating system to the English method, and claimed in Book 1, chapter 5, section 2, that his system was based on the rules of the Greeks and Romans (Cordoliani 1960, 334 and footnote 38)
Dicuil must have been familiar with the book by Boethius (c. 500) De institutione arithmetica (On arithmetic) (Masi 1983; Oosthout and Schilling 1999), which was widely available in Western Europe. Boethius wrote in Latin, but based his book on earlier Greek authors such as Theon of Smyrna and Nicomachus. The Introduction to arithmetic by Nicomachus was translated into Latin by Apuleius in the second century (Midonick 1968, 15–16), and Boethius probably had access to this. Boethius discusses figurate numbers in Book II. He states that triangular numbers are the basis of all other figurate numbers (chapters 6 and 18). Unity is the mother of all numbers, and not a real triangular number: 3 is the first triangular number, and has 2 as a side; 6 is the second and has 3 as a side; the sides grow by unity (chapters 7 and 8). The sequence of triangular numbers grows by addition of the natural numbers (chapter 9). Later chapters deal with square numbers and other figurate numbers. He describes rectangular or heteromecic numbers (chapter 26), and says that the sum of two consecutive triangular numbers is a square number (chapters 18 and 28); but he does not give the multiplication formula, or state that a rectangular number is twice a triangular number. However, these formulae can readily be deduced from this book, so Dicuil probably benefitted from reading Boethius
Cassiodorus (c. 485–585) wrote Institutions of divine and secular learning, and on the soul (Halporn and Vessey 2004) in which he briefly mentioned triangular
numbers (Book 2, Part 4, Section 6), but not the multiplication formula. This book was not widely used or cited by Carolingian authors (Halporn and Vessey 2004, 82). Butzer (1993) concludes that the major mathematical contributions of the Carolingian period were: the pseudo-Boethian Geometry I, perhaps produced in Corbie (c.780– 800); the Libellus annalis of 793, a precursor of the Computus of 809, probably written by Alcuin; the Seven Book Computus, assembled at Aachen 809/10; and the Propositiones ad acuendos iuvenes, the oldest collection of mathematical exercises written in Latin, probably by Alcuin. We shall now turn our attention to the last of these, because it contains an example of relevance to the multiplication formula
A different tradition from the mathematical textbook lay in collections of practical problems and riddles. The multiplication formula can be used for the sum of the natural numbers in other contexts besides triangular numbers. One example occurs in Propositiones ad acuendos juvenes (Problems to sharpen the young), an early collection of recreational mathematical problems (Folkerts 1978; Hadley and Singmaster 1992; Folkerts and Gerike 1993). Problem 42 is of particular interest. It is entitled Propositio de scala habente gradus centum ( Problem concerning a staircase with a hundred steps )
A version of the multiplication formula was indeed known to the Egyptians, as early as 300 BC (Gillings 1978; Høyrup 2008). A papyrus in the British Museum contains mathematical problems, including the sum of the arithmetical progression formed by the natural numbers
Here is the translation of Dicuil's 9th century text:

Speculating whether or not Dicuil could have read Greek texts containing the use or mention of figurates can allow one to make a logical inference that he did indeed, but real question is, if he didn't list his sources, how can we reasonably infer what they were, and if not, where at least they may have come from, and who passed the knowledge down
We can do this by starting with the school the Dicuil taught at, the Carolingian school of Louis the Pious
Louis the Pious (778 – 20 June 840), also called the Fair, and the Debonaire, was the King of the Franks and co-emperor with his father, Charlemagne, from 813
He had a twin brother named Lothair, who died young. Louis and Lothair were given names from the old Merovingian dynasty, possibly to suggest a connection

Under the Merovingian Kings of the Frankish kingdoms there was established at the court a 'palatial' school -- scola palatina, the chroniclers of the eighth century styled it—for the training of the young Frankish nobles in the art of war and in the ceremonies of the court
With the accession of the future emperor Charlemagne (768) a scheme of educational reform was inaugurated, first in the palace school itself, and later in the various schools established or reformed by imperial decrees throughout the vast empire over which Charlemagne reigned. The reform of the palace school, i.e. the change from a school of military tactics and court manners to a place of learning, was begun in 780, as soon as the victories over the Lombards, Saxons and Saracens (in Iberia) afforded
Associated with the extension and promotion of the Carolingian revival of education are the names of various Irish teachers, competitors of Alcuin, who certainly share in the credit of having been the first masters of the schools. According to the St. Gall chronicler who wrote the Life of Charlemagne dedicated to Charles the Fat (d. 888), two Irish monks arrived in France before Alcuin had received Charlemagne's invitation. Having set out their stall in the marketplace to somewhat boastfully teach wisdom, they were received by the emperor with honour, and one of them placed at the head of the palace school. The story, however, is not accepted as entirely reliable.
We know for certain that after Alcuin left the court of Charlemagne, one of these monks Clement the Irishman (Clemens Scotus) succeeded him as master of the palace school, and that he had pupils sent to him even from the monastery of Fulda. The grammarian Cruindmelus, the poet Dungal of Bobbio and Bishop Donatus of Fiesole were among the many Irish teachers on the Continent who enjoyed the favour of Charlemagne. The anonymous Hibernicus exul also wrote at his court. Indeed, the emperor, according to Einhard, "loved the strangers" and "had the Irish in special esteem".
His successors likewise invited the Irish teachers to their court. Louis the Pious was the patron of the Irish geographer Dicuil, Lothair II stood in a similar relation to the Irish poet and scribe Sedulius Scottus, founder of the school at Liège, and Charles the Bald equalled his grandfather in his affectionate esteem for the Irish teachers. Under him Elias taught at Laon, Dunchad at Reims, Israel at Auxerre, and the greatest of all the Irish scholars, Johannes Scotus Eriugena, was head of the palace school.
Naturally the Irish teachers flocked to the places already known to them by the missionary activity of their fellow-countrymen of former generations We find them at Reichenau, St. Gall and Bobbio, "a whole herd of philosophers" as a ninth-century writer expresses it. Every monastery or cathedral school at which they appeared soon showed the effect of their influence. To the curriculum already in vogue in the Carolingian Schools the Irish teachers added the study of Greek, and wherever they taught philosophy or theology (dialectic and the interpretation of the Scriptures) they drew largely from the writings of the neo-Platonists and from the works of the Greek Fathers
Neo-Platonists seem to originate with Ammonius Saccas and his student Plotinus (c. 204/5 – 271 AD) and which stretches to the 5th century AD
Those who wrote in Greek are called the Greek (Church) Fathers. In addition to the Apostolic Fathers, famous Greek Fathers include: Justin Martyr, Irenaeus of Lyons, Clement of Alexandria, Athanasius of Alexandria, John Chrysostom, Cyril of Alexandria, the Cappadocian Fathers (Basil of Caesarea, Gregory Nazianzus, Gregory of Nyssa), Peter of Sebaste, Maximus the Confessor, and John of Damascus.
Justin Martyr c. 100 – c. 165
John of Damascus c. 675 - c 749
Hibernicus exul (fl. 8th century) was an anonymous Irish Latin poet, grammarian, and dialectician. His works include a comic mock epic, a panegyric to Charlemagne, epigrams of advice to young scholars and a poetic overview of the seven liberal arts
Dungal of Bobbio (fl. 811–828) was an Irish monk, teacher, astronomer, and poet. He was to live at Saint-Denis, Pavia, and Bobbio
He may be the same person as Hibernicus exul. A letter of Alcuin appears to identify him as a bishop
Saint Donatus (Donat, Donnchad) of Fiesole was an Irish teacher and poet, and Bishop of Fiesole, about 829–876
John Scotus Eriugena or Johannes Scotus Erigena (c. 800 – c. 877) was an Irish theologian, neoplatonist philosopher, and poet. He succeeded Alcuin of York (735–804) as head of the Palace School at Aachen
Bertrand Russell called him " the most astonishing person of the ninth century "
A tradition, largely considered spurious, says he was stabbed to death by his students at Malmesbury with their pens
He also translated and made commentaries upon the work of Pseudo-Dionysius, and was one of the few Western European philosophers of his day who knew Greek, having studied in Byzantine Athens
Johannes Scotus Eriugena was an Irishman, educated in Ireland. He moved to France (about 845) and took over the Palace School at the invitation of Carolingian King Charles the Bald. He succeeded Alcuin of York (735–804) as head of the Palace School. The reputation of this school, part of the Carolingian Renaissance, seems to have increased greatly under Eriugena's leadership, and the philosopher himself was treated with indulgence by the king. Whereas Alcuin was a schoolmaster rather than a philosopher,...
Eriugena was a noted Greek scholar, a skill which, though rare at that time in Western Europe, was used in the learning tradition of Early and Medieval Ireland, as evidenced by the use of Greek script in medieval Irish manuscripts
He remained in France for at least thirty years, and it was almost certainly during this period that he wrote his various works
However, what we can say is that Dicuil most likely would have learned Greek from Eriugena, being that he was a notable Greek scholar and also head of the school Dicuil himself taught at
Aachen developed from a Roman settlement and spa, subsequently becoming the preferred medieval Imperial residence of Emperor Charlemagne of the Frankish Empire,and, from 936 to 1531, the place where 31 Holy Roman Emperors were crowned Kings of the Germans
Aachen is a city of North Rhine-Westphalia
Lower Saxony : Neddersassen; Saterland Frisian: Läichsaksen) is a German state (Land) situated in northwestern Germany
Lower Saxony borders on (from north and clockwise) the North Sea, the states of Schleswig-Holstein, Hamburg, Mecklenburg-Vorpommern, Brandenburg, Saxony-Anhalt, Thuringia, Hesse and North Rhine-Westphalia, and the Netherlands (Drenthe, Groningen and Overijssel)
Elias taught at Laon, Dunchad at Reims, Israel at Auxerre
scribe Sedulius Scottus, founder of the school at Liège
The Merovingian dynasty (/ˌmɛrəˈvɪndʒiən/) was the ruling family of the Franks from the middle of the 5th century until 751, being succeeded by the Carolingian dynasty
Curiously, there is a stark juxtaposition between the Merovingians and the Carolingians
Unlike the Anglo-Saxon royal genealogies, the Merovingians never claimed descent from a god, nor is there evidence that they were regarded as sacred
A number of royal genealogies of the Anglo-Saxon kingdoms, collectively referred to as the Anglo-Saxon royal genealogies, have been preserved in a manuscript tradition based in the 8th to 10th centuries
The genealogies trace the succession of the early Anglo-Saxon kings, back to the semi-legendary kings of the Anglo-Saxon settlement of Britain, notably named as Hengest and Horsa in Bede's Historia ecclesiastica gentis Anglorum, and further to legendary kings and heroes of the pre-migration period, usually including an eponymous ancestor of the respective lineage and converging on Woden ( Odin ). In their fully elaborated forms as preserved in the Anglo-Saxon Chronicles and the Textus Roffensis, they continue the pedigrees back to the biblical patriarchs Noah and Adam. They also served as the basis for pedigrees that would be developed in 13th century Iceland for the Scandinavian royalty
Odin is known in Old English and Old Saxon as Wōden, in Old Dutch as Wuodan, and in Old High German as Wuotan, all ultimately stemming from the Proto-Germanic theonym *Wōđanaz, meaning 'lord of frenzy', or 'leader of the possessed'
Old Norse texts portray Odin as one-eyed and long-bearded, frequently wielding a spear named Gungnir and wearing a cloak and a broad hat. He is often accompanied by his animal companions and familiars—the wolves Geri and Freki and the ravens Huginn and Muninn, who bring him information from all over Midgard—and rides the flying, eight-legged steed Sleipnir across the sky and into the underworld
Odin appears as a prominent god throughout the recorded history of Northern Europe, from the Roman occupation of regions of Germania (from c. 2 BC ) through movement of peoples during the Migration Period (4th to 6th centuries AD ) and the Viking Age (8th to 11th centuries AD )
Ross, H. E., & Knott, B. I. (2019). Dicuil (9th century) on triangular and square numbers. British Journal for the History of Mathematics, 34(2), 79–94. doi:10.1080/26375451.2019.1598687
www.tandfonline.com/doi/abs/10.1080/26375451.2019.1598687
---------------------
An Irish Teacher at the Carolingian Court: Dicuil
Mario Esposito
www.jstor.org/stable/30092449?seq=1
---------------------
en.wikipedia.org/wiki/Alcuin
Quadrivium
-------------------------------------------------------------------------
Make two lists: Authors and publications , dated
Methods and formulas , dated
-------------------------------------------------------------------------
...
Bible moralisée
There are seven surviving fully illustrated manuscripts of the Bible moralisée group;all date from the thirteenth to the fifteenth centuries and were designed for the personal use of the French royal family
--------
Moon
--------
Sun
------------------
Distances - aphelion, LDU, etc
--------------
Times
-----------------
Gravity
-----------
eclipses
-------------