I am not a mathematician, by any means, but I started trying to teach myself about it after I retired 10 years ago. One of the things I do is engage in " recreational math ", this is really just more of an exercise for my mind, but also to help educate me about math / math history / etc
One of the things I played around with is what are called " orbits " or " loops " in the digits of pi,, I've also seen them referred to as " self-locating strings "
" Number of iterations of A176341 ("position of n in Pi") until a value is reached for the second time, when starting with n, or -1 if no value is repeated "
oeis.org/A232013 Example: If you search for 169, it appears at position 40. If you then search for 40, it appears at position 70. Search for 70, ... and so on, after some number of iterations you loop back to the same starting point:
40, 70, 96, 180, 3664, 24717, 15492, 84198, 65489, 3725, 16974, 41702, 3788, 5757, 1958, 14609, 62892, 44745, 9385, 169, 40
The occurrence of loops, I would expect, would be random, since the digits of pi have been shown to be random, and this is also true if we did this for something like the digits of another constant like e or phi ( I'm inferring there )
Naturally, since I have a short attention span, I got sidetracked
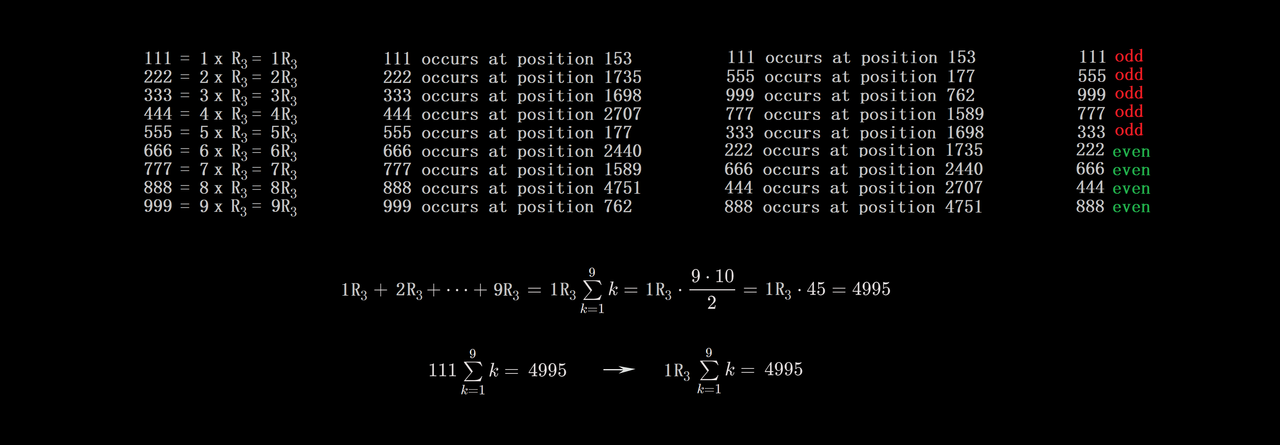
I've spent a few years investigating the use of repunits and repdigits combined with figurate numbers, for the purpose of mathematical astronomy in the antiquities ( Something I believe was included in priestly corpuses ), and in the spirit of recreational math, I started looking at repunits and repdigits as they occur in pi . Along with this I started to learn a little about distributions and probabilities, so I know that the probability of finding a given string of digits in pi shrinks with the increasing number of digits in the term
Now, if pi digits are random, and loops in pi digits are random, then if I did something like take the repdigits ( 1,11,111,1111...9,99,999,9999 ... ) and write their positions in pi digits in columns, iow
1 occurs at position 1
2 occurs at position 6
3 occurs at position 9
...
then repeated this for repdigits up to six digits in length ( 111111, 222222, ...,888888,999999 ) then took those columns and re-wrote them such they are arranged in descending order of smallest to largest position number of the terms in pi digits, I should expect that the distribution of even and odd repdigits in the columns would be randomized as well, right ?
I'm assuming it should be random, since mixing something that's already random should just produce something that's also randomized
Yet, this is not true for 3 digit repdigit terms in pi digits

Then this can be narrowed down to the set used for Hebrew and Greek
2
A mathematical formula for finding a letter's corresponding number in Hebrew Mispar Gadol, where x is the position of the letter in the language letters index (regular order of letters), and the floor and modulo functions are used
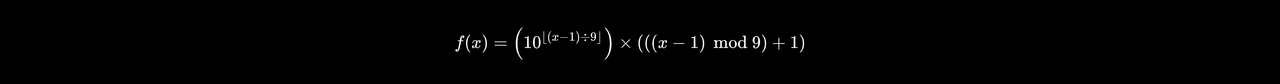
The modulo operation returns the remainder or signed remainder of a division, after one number is divided by another (called the modulus of the operation)
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book Disquisitiones Arithmeticae, published in 1801.
A familiar use of modular arithmetic is in the 12-hour clock, in which the day is divided into two 12-hour periods ( A " watch " in Mesopotamian time )
If the time is 7:00 now, then 8 hours later it will be 3:00. Simple addition would result in 7 + 8 = 15, but clocks "wrap around" every 12 hours. Because the hour number starts over after it reaches 12, this is arithmetic modulo 12. In terms of the definition below, 15 is congruent to 3 modulo 12, so "15:00" on a 24-hour clock is displayed "3:00" on a 12-hour clock.
Mispar Gadol means Large Number