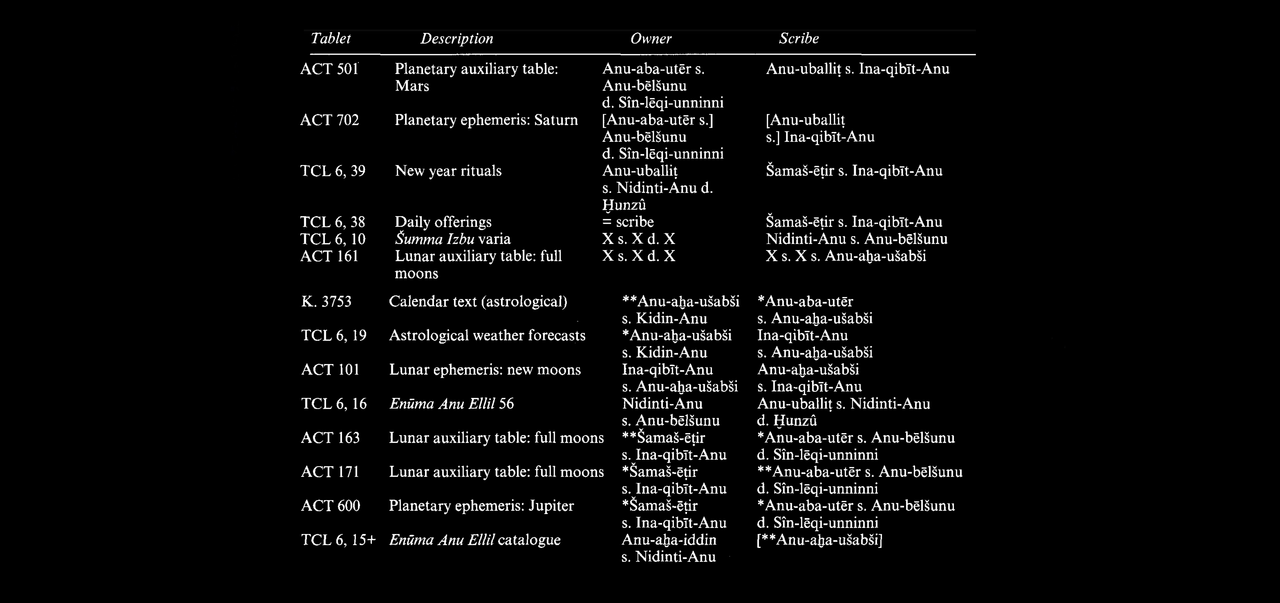
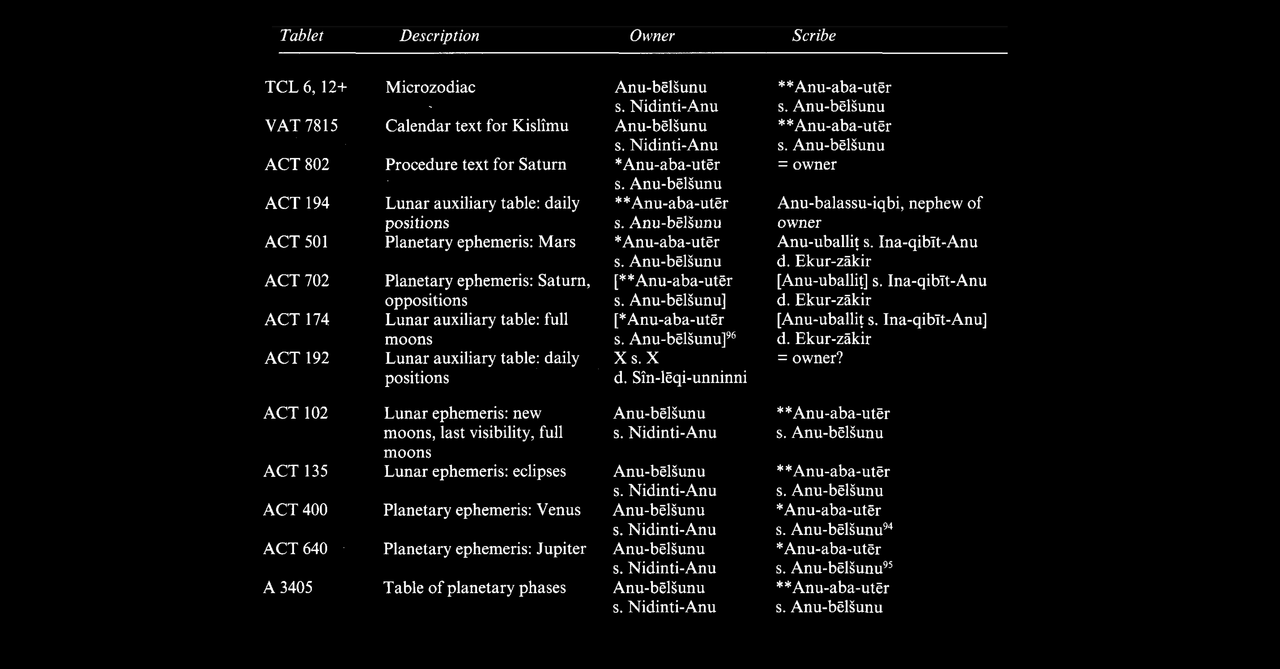
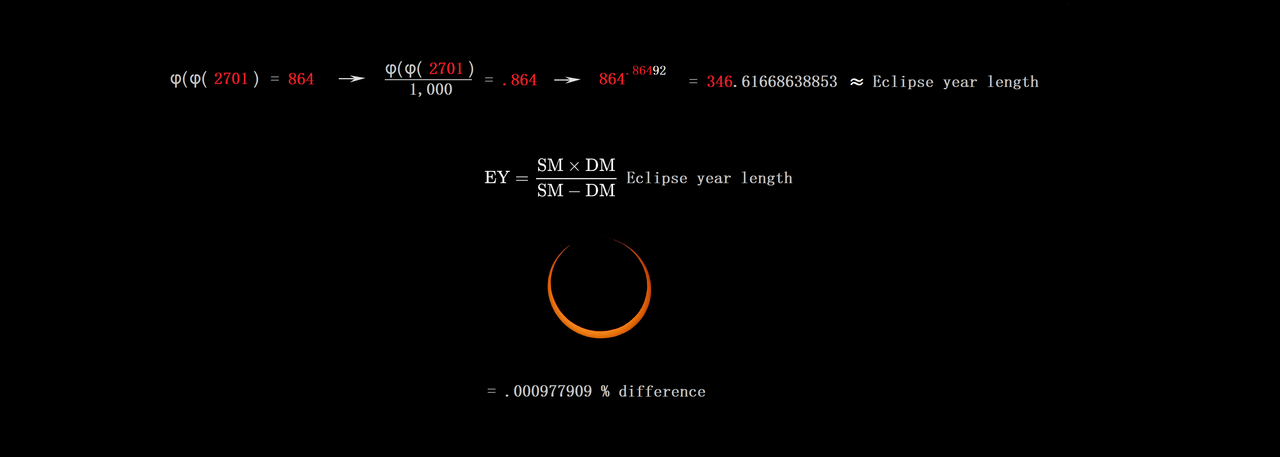
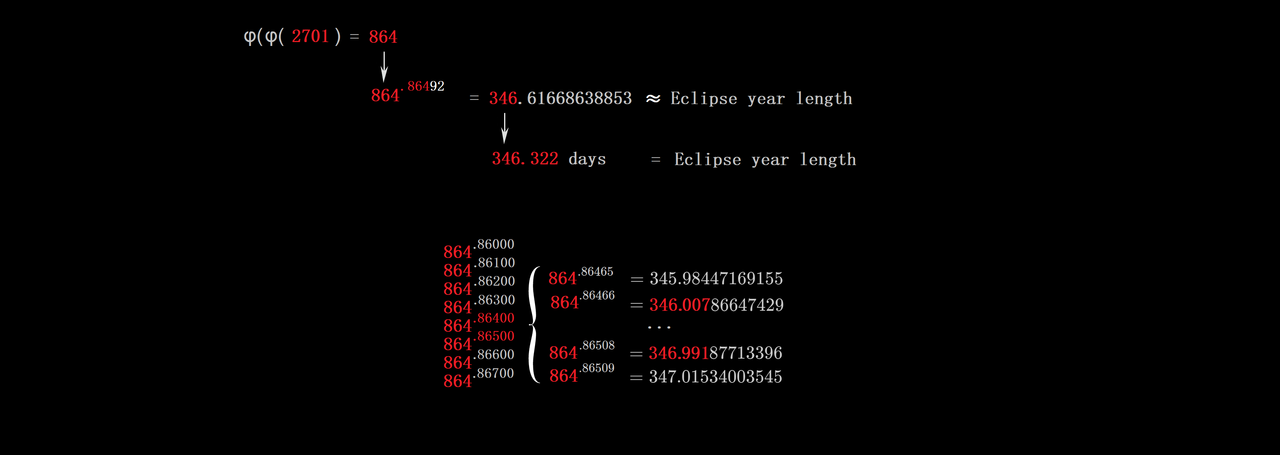
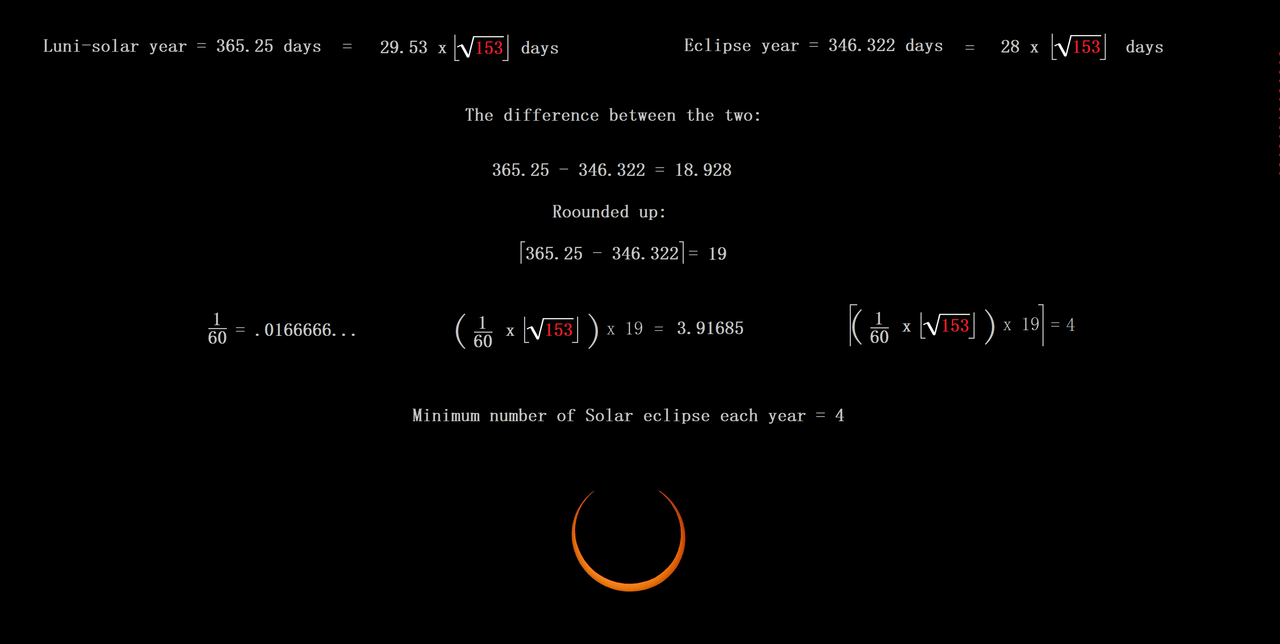
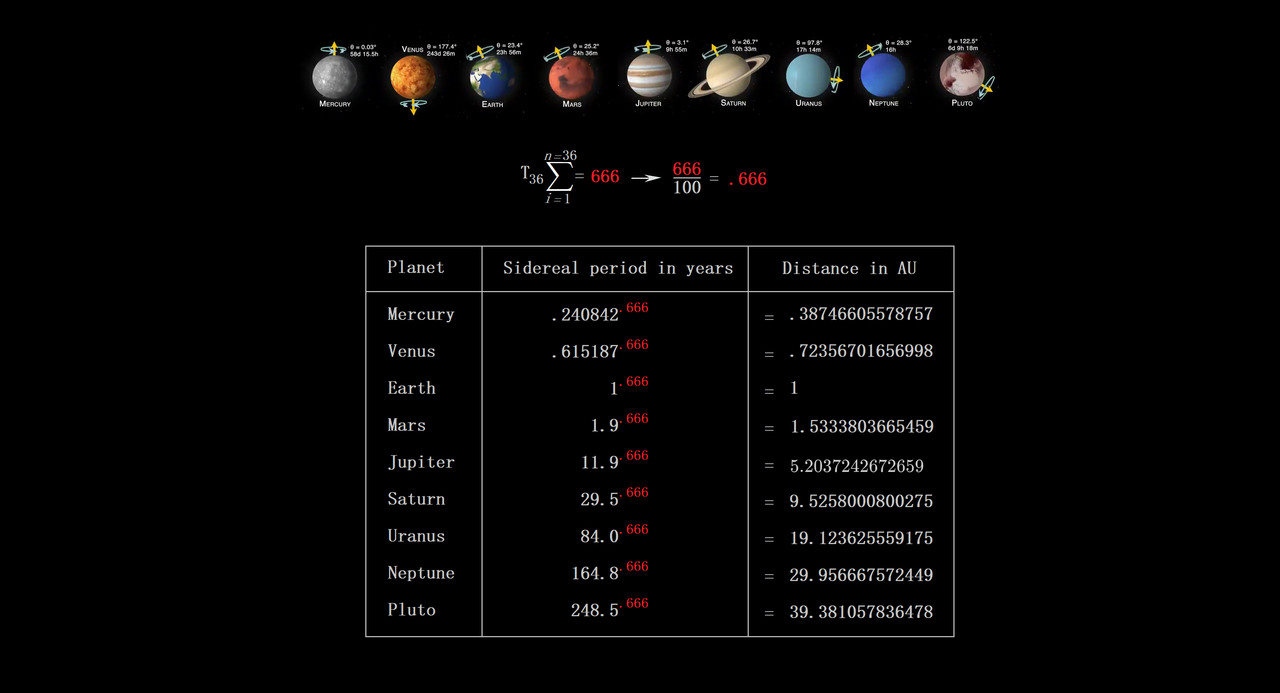
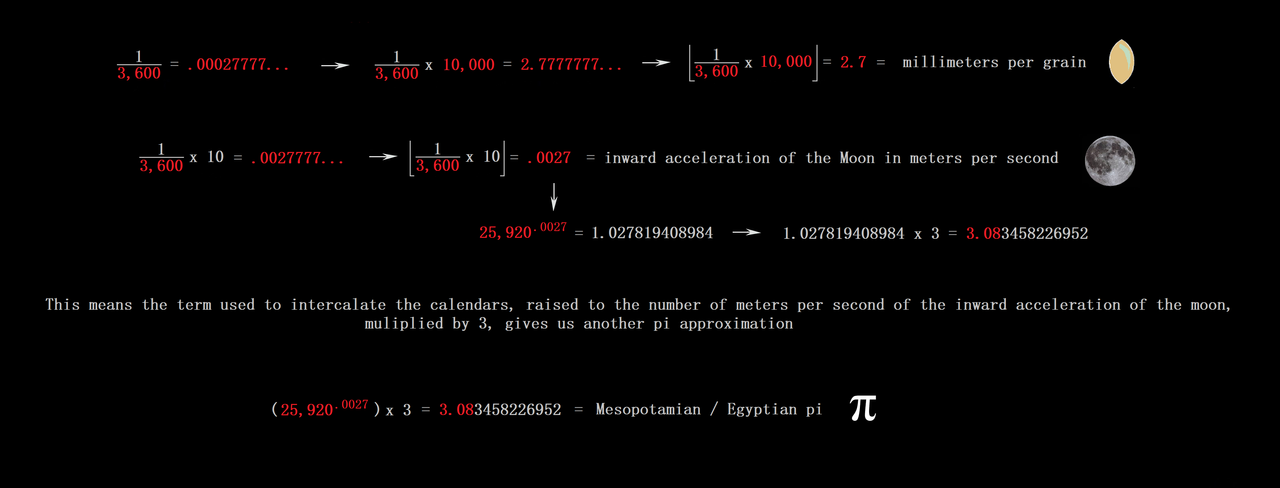
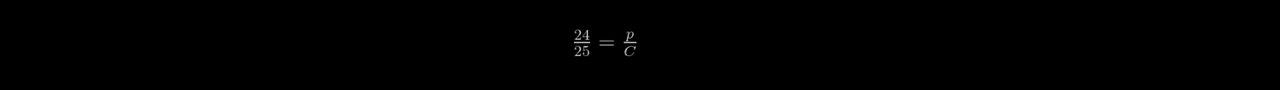Astrometry With Pi and Figurate Numbers Like 666
Feb 24, 2021 18:15:54 GMT
Post by Admin on Feb 24, 2021 18:15:54 GMT
.

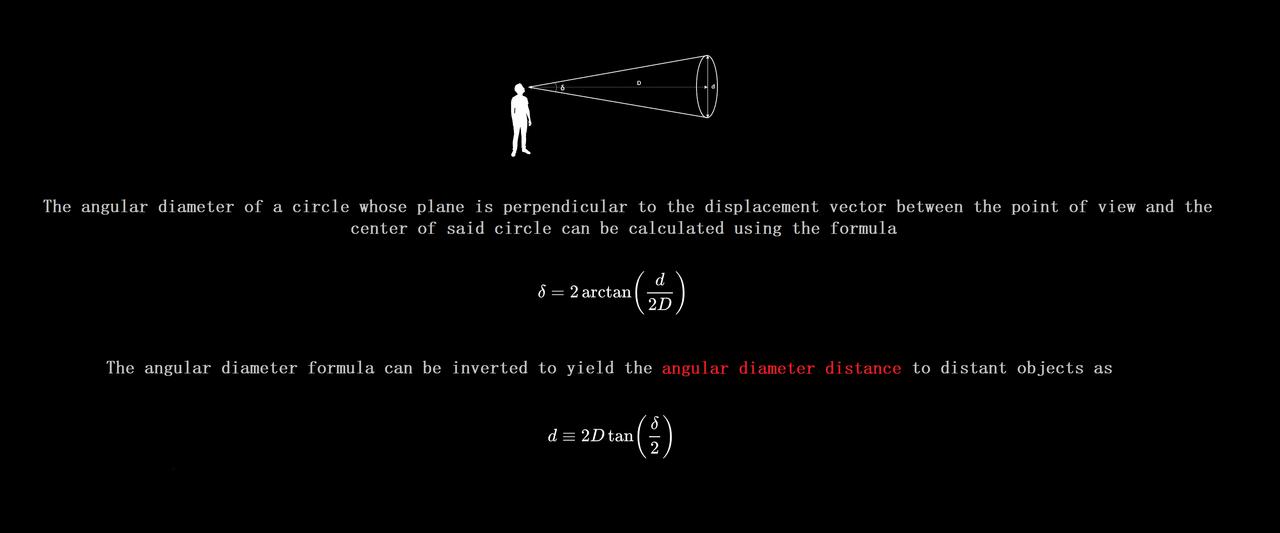
...

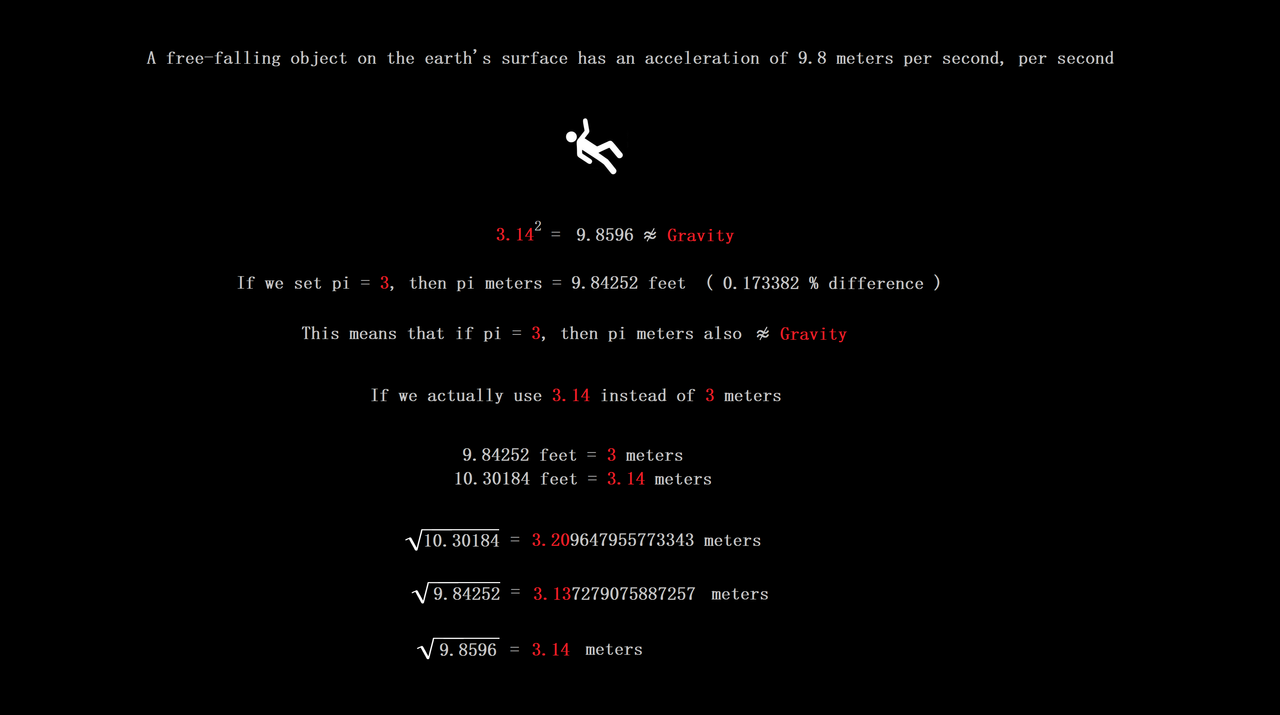
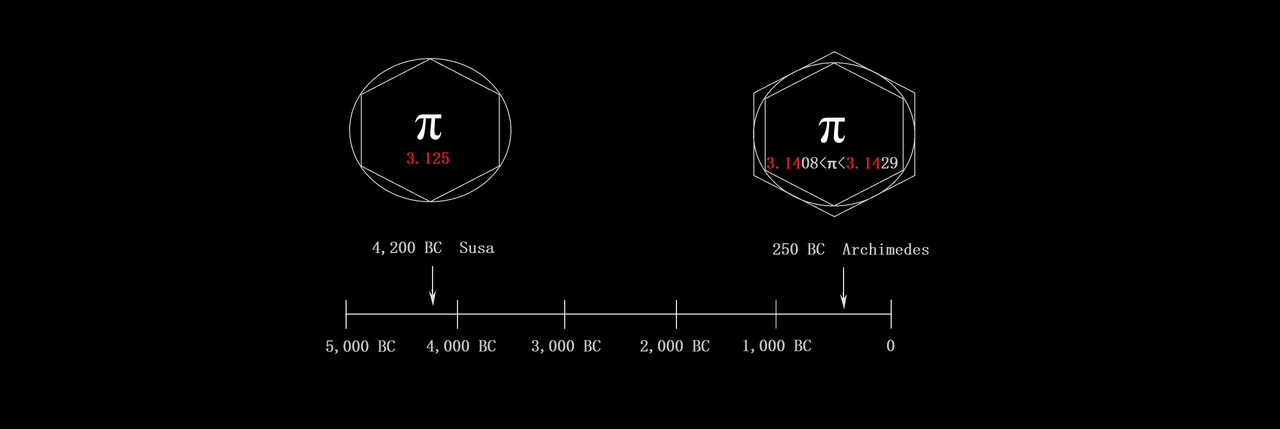
Let's first look at why it's actually OK to use a pi that equals something like 3 or 3.1
It's all to common that I hear people online in chats and forums mocking the apparent value of ~3 for pi that's given in the Bible, like it's some sort of proof that whoever wrote it was a drooling moron
It's all to common that I hear people online in chats and forums mocking the apparent value of ~3 for pi that's given in the Bible, like it's some sort of proof that whoever wrote it was a drooling moron

I've even had people tell me to " Plug pi = 3 into a CAD program and see what happens "
Right..., now I'm going to now show you who the " drooling morons " really are
Let's start by talking measurements of angular diameter and angular distance, in astronomy
Let's start by talking measurements of angular diameter and angular distance, in astronomy

...

We're going to use angular diameter to measure the distance to the moon, and we're going to use pi = 3
Knowing the moon's true diameter (1/4 that of the earth), we can use its measured angular diameter (half a degree) to determine its distance. Qualitatively, the idea is this: For a given true size, a larger angular diameter would mean that the moon must be closer; whereas a smaller angular diameter would mean that the moon must be farther away. Because we know the moon's angular diameter, we can calculate just how far it is
The calculation takes a few steps, and requires some effort and practice to fully understand. But similar calculations come up so often in astronomy that it's a good investment to start practicing now
A useful trick for visualizing the calculation is to sketch a big, imaginary circle, centered on you (the observer), passing through the moon. Then label the angle that represents the moon's measured angular width (half a degree in reality, but it's fine to exaggerate it in the picture as I have). Also label the moon's known diameter, 1/4 (in units of earth's diameter)
The calculation proceeds in three steps:
Ask yourself how many hypothetical moons it would take, placed side by side, to reach all the way around the circle. Since a full circle is 360° but each moon takes up only 1/2°, the answer is 360 divided by 1/2, or 720 hypothetical moons
Now calculate the circumference of the circle. Since each moon has a width of 1/4 e.d., and it takes 720 of them to go all the way around, the answer is 720 times 1/4 e.d., or 180 earth diameters. (You could use units of miles instead of earth diameters if you prefer, but then the numbers get a little more cumbersome: 720 × 2000 = 1,440,000.)
The distance to the moon is the radius of the circle

But for any circle, the circumference is 2π times the radius, where π is a number that's equal to a little more than 3. If you don't need an especially accurate answer,
it's fine to pretend that π equals 3 and just say that the circumference is six times the radius
Then the radius (or distance) is simply the circumference divided by 6, or in this case, 180 earth diameters divided by 6, or 30 earth diameters
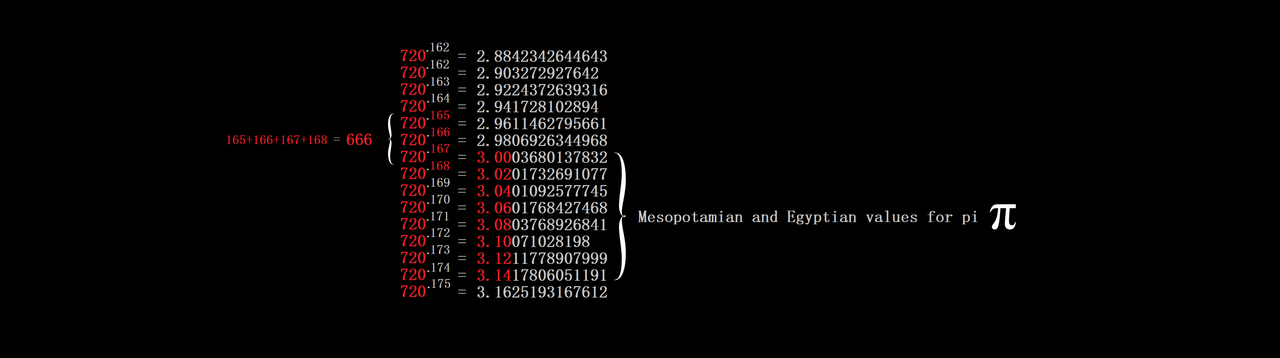
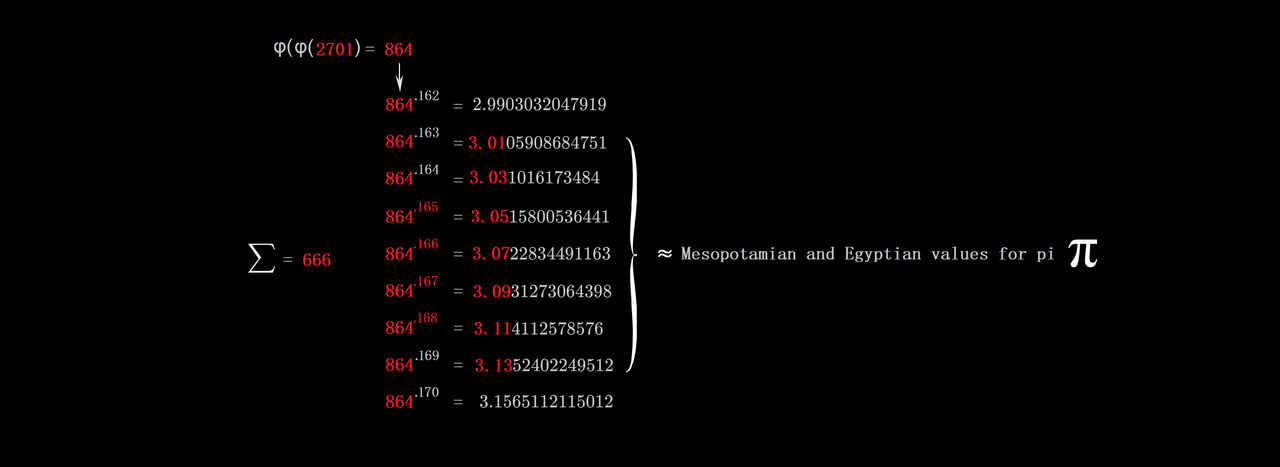
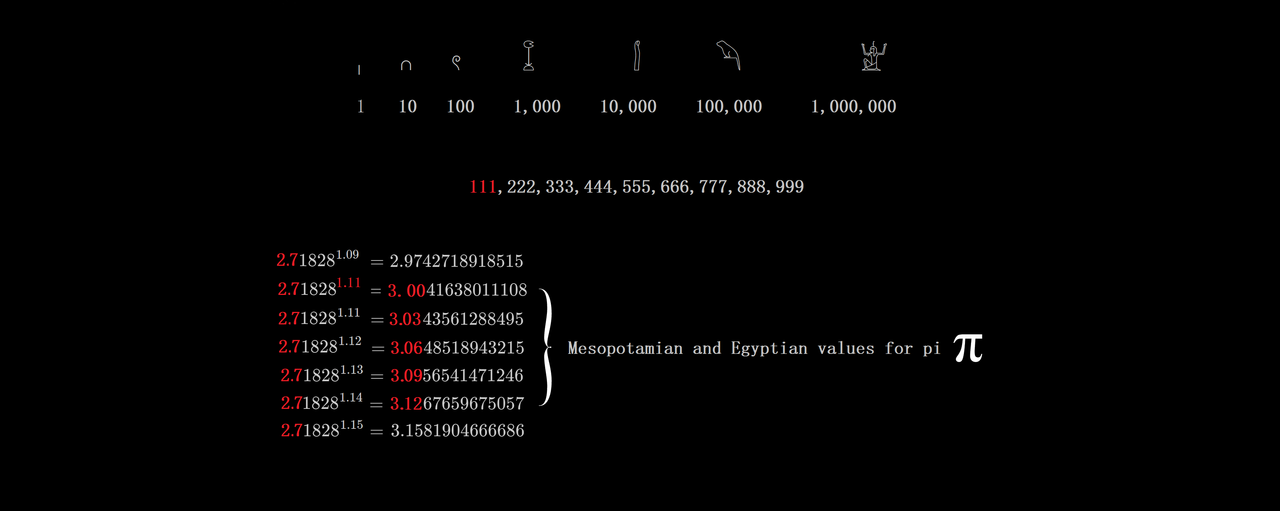
So, it turns out that people mocking the Bible's value of pi as ~ 3, or attempting to ridicule those ancient silly savages like the Mesopotamians and Egyptians,...well,.....apparently they don't grasp simple math or how it applies in astrometry
If you happen to be one of those mockers....Congratulations, your " argument " is null and void, and not only that, you're nowhere near as educated as you think yourself to be
It always blows my mind that when I see people " debating " about this online, they basically ignore that it's completely OK to use a pi that = 3 or 3.1 or 3.01 or so on, even though this is common in engineering with B.O.T.E. calculations
A B.O.T.E., is a back-of-the-envelope calculation, a rough calculation, typically jotted down on any available scrap of paper such as an envelope. It is more than a guess but less than an accurate calculation or mathematical proof
You don't need extreme accuracy for calculations involving approximations in measurement, and people that think this, and say things like " Oh yeah ? Plug pi = 3 into a CAD program " might actually need to go back and start math at the grade school level

==============
Notes
Explanation of calculating distance to the moon is from this website - physics.weber.edu/schroeder/ua/MoonAndEclipses.html
Knowing the moon's true diameter (1/4 that of the earth), we can use its measured angular diameter (half a degree) to determine its distance. Qualitatively, the idea is this: For a given true size, a larger angular diameter would mean that the moon must be closer; whereas a smaller angular diameter would mean that the moon must be farther away. Because we know the moon's angular diameter, we can calculate just how far it is
The calculation takes a few steps, and requires some effort and practice to fully understand. But similar calculations come up so often in astronomy that it's a good investment to start practicing now
A useful trick for visualizing the calculation is to sketch a big, imaginary circle, centered on you (the observer), passing through the moon. Then label the angle that represents the moon's measured angular width (half a degree in reality, but it's fine to exaggerate it in the picture as I have). Also label the moon's known diameter, 1/4 (in units of earth's diameter)
The calculation proceeds in three steps:
Ask yourself how many hypothetical moons it would take, placed side by side, to reach all the way around the circle. Since a full circle is 360° but each moon takes up only 1/2°, the answer is 360 divided by 1/2, or 720 hypothetical moons
Now calculate the circumference of the circle. Since each moon has a width of 1/4 e.d., and it takes 720 of them to go all the way around, the answer is 720 times 1/4 e.d., or 180 earth diameters. (You could use units of miles instead of earth diameters if you prefer, but then the numbers get a little more cumbersome: 720 × 2000 = 1,440,000.)
The distance to the moon is the radius of the circle

But for any circle, the circumference is 2π times the radius, where π is a number that's equal to a little more than 3. If you don't need an especially accurate answer,
it's fine to pretend that π equals 3 and just say that the circumference is six times the radius
Then the radius (or distance) is simply the circumference divided by 6, or in this case, 180 earth diameters divided by 6, or 30 earth diameters
So, it turns out that people mocking the Bible's value of pi as ~ 3, or attempting to ridicule those ancient silly savages like the Mesopotamians and Egyptians,...well,.....apparently they don't grasp simple math or how it applies in astrometry
If you happen to be one of those mockers....Congratulations, your " argument " is null and void, and not only that, you're nowhere near as educated as you think yourself to be
It always blows my mind that when I see people " debating " about this online, they basically ignore that it's completely OK to use a pi that = 3 or 3.1 or 3.01 or so on, even though this is common in engineering with B.O.T.E. calculations
A B.O.T.E., is a back-of-the-envelope calculation, a rough calculation, typically jotted down on any available scrap of paper such as an envelope. It is more than a guess but less than an accurate calculation or mathematical proof
You don't need extreme accuracy for calculations involving approximations in measurement, and people that think this, and say things like " Oh yeah ? Plug pi = 3 into a CAD program " might actually need to go back and start math at the grade school level

==============
Notes
Explanation of calculating distance to the moon is from this website - physics.weber.edu/schroeder/ua/MoonAndEclipses.html